(順相関)
(正の相関)
に近くなる
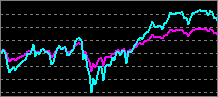
に近くなる
(逆位相関)
(負の相関)
に近くなる
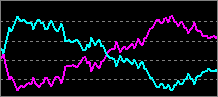
相関関係は大きく「順位相関」「無相関」「逆相関」の3種類に分類できます。
| 相関関係の種類 | 相関係数 | 為替レートのグラフ例 | 特徴 |
|---|---|---|---|
| 順位相関 (順相関) (正の相関) |
+1 に近くなる |
 |
2通貨ペアが似た動きをする。 |
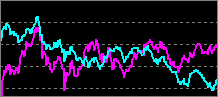
| 無相関 | 0 に近くなる |
 |
2通貨ペアの動きに関係性は無い。 |
| 逆相関 (逆位相関) (負の相関) |
-1 に近くなる |
 |
2通貨ペアは逆の動きをする。 |
2通貨ペアがどちらとも同じ(通貨ペアA = USDJPY かつ 通貨ペアB = USDJPY など)場合、相関係数は1となり、完全な「順位相関」となります。このような特殊なケースを除けば、完全に「順位相関」というケースは皆無です。実際には -1 ~ +1 までの数値で表される相関係数で相関関係を表現します。相関関係の種類と相関係数との関係は上表の通りですが、中間の値を含めて、下記のような分類をします。
| 相関係数 | 分類 | ||
|---|---|---|---|
| +0.75 | ~ | +1 | 強い順位相関 |
| +0.5 | ~ | +0.75 | 中度の順位相関 |
| +0.2 | ~ | +0.5 | 弱い順位相関 |
| -0.2 | ~ | +0.2 | 無相関 |
| -0.5 | ~ | -0.2 | 弱い逆相関 |
| -0.75 | ~ | -0.5 | 中度の逆相関 |
| -1 | ~ | -0.75 | 強い逆相関 |
なお、相関係数の範囲や分類は諸説あり、上記はその一例です。
相関係数は統計学的な順序尺度(ordinal scale)です。
順序尺度とは、スポーツの順位のようなものです。つまり、相関係数の大小を比較することは意味がありますが、複数の相関係数を掛け合わせて計算すること(たとえば、平均を求めたり、何倍の相関関係があるか考えること)は意味がありません。
スポーツで2位の選手と6位の選手では、2位の選手のほうが強いと考えるのは一般に妥当です。でも、2位と6位の選手の実力に3倍の差があるとは限りませんよね。また、4位の選手は2位と6位の選手の実力を足して2で割った(=平均)実力があるとは限りませんよね。
これこそが、難しいところですが、
などといった、考え方があります。
いずれにしても、何らかの要因で予想外の急変動をするリスクはあります。そのため、1つの組み合わせだけでなく、複数の組み合わせに分散させることが重要です。その際には、急変動したときに同じ方向性の変動をしないように、異なる通貨で構成することがポイントです。